Difference between Money Weighted Return and Time Weighted Return?
Very often students of
finance are confused between Time
Weighted Return and Money Weighted
Return. In this article we have tried to clarify both of them and also show
how both these type of returns differ from each other.
This article highlights
how the timing of the returns earned on the portfolio affects the overall financial
position. In other words it is not just the size of the returns that has to be
considered but also the timing of the returns while assessing the overall
returns on the portfolio. We would explain this phenomenon with the help of examples covering two 2
concepts-Time Weighted Rate of Return and Money Weighted rate of Return.
Time Weighted Return (TWR)
It allows an investor to
directly measure their portfolio’s true performance and compare the
performances of different money managers over a given time frame.It
computes the return for each period and takes the average of the results. It
finds the holding period for each period and averages them. If the investment
is for more than one year, the geometric mean of the annual returns is taken to
find the time-weighted rate of return for the measurement period.
Let us explain this with an example:
Suppose we have 3 annual returns of -10%, +15% and +5% then
the average (time weighted) return after the 3 years can be calculated as
follows:
Average time-weighted = [(1+ r1) ´
(1+r2)´ (1+r3)]^(1/3)-1
=
[(1-10%) ´ (1+15%) ´
(1+5%)]^(1/3)-1
=
[0.9´ 1.15 ´ 1.05]^(1/3)-1
=
2.81% per annum
It is interesting to note that when working with time weighted
returns, the order in which the returns occur does not matter. Let us change r1
and r3 around. Then we get:
Average
time-weighted = [(1+5%) ´ (1+15%) ´
(1-10%)]^(1/3)-1
= [1.05 ´ 1.15´
0.9]^(1/3)-1
= 2.81%
per annum
We get the same answer because we have applied the same weighting
to each return item, which in this case, was based on the amount of time it
applies to i.e. one year. Hence the name “time-weighted”
returns.
In general, the arithmetic and time-weighted average returns do
not provide the same answers, because computation of the arithmetic average
assumes the initial amount invested to be maintained (through additions or
withdrawals) at its initial investment value. The time weighted return, on the
other hand, is the return on a portfolio that varies in size because of the
assumptions that all proceeds are reinvested.
Money-Weighted Return
When it comes to what one actually ends up with in his/herkitty,
time-weighted returns is mostly irrelevant. This is wheremoney-weighted return
is the correct measure of returns and this is where the timing of the returns
affects the final result.It is defined as the internal rate of return on a
portfolio taking into account all cash inflows and outflows. The IRR is the
discount rate that equates the ending investment with the compounded value of
the beginning market value as well as all net contributions made during the
life of the investment.
The
MWRR can be calculated by solving the expression below for r(T)...
MW(T) = MV(0)´ {1+r(T)}T + sum [C(t)´
{1+r(T)}{T-t}]
MW(T) : Ending market value portfolio
MW(0) : Beginning market value portfolio
T : Ending time T
r(T) : IRR at time T over time period {0,T}
C(t) : Net contribution at time t
Note
that the time period (0,T) is assumed to be divided in n equally spaced time
periods. Other formulas with different time conventions exist.
Let us look at two
different members of the same retirement fund.
Mr.
A just started his first job and has started saving towards retirement. His
starting assets are therefore Rs 0. Let us furtherassume that he contributes Rs10
000 at the end of each of the next 3 years. Mr. B is nearing retirement and
thus far accumulated Rs750 000. He also contributes Rs10 000 at the end of each
of the next 3years.Both Mr. A and Mr. B are invested in the same balanced fund.
Scenario 1
Now
let us assume the annual returns on the balanced fund over the following 3
years are:
Year
1 -10%
Year
2 +15%
Year 3 +5%
What
is the average return earned on their assets? And what are the total assets
after 3 years?
For
Mr. A his total assets are Rs32575.00 which implies an average money-weighted
return of 8.35% per annum.
For
Mr. B his total assets are Rs847637.50 which implies an average money-weighted
return of 2.88% per annum.
Scenario 2
Now let us change the annual returns of year 1 and year 3 around
and perform the same calculations:
Year 1 +5%
Year 2 +15%
Year 3 -10%
What is the average return earned on their assets? And what are
the total assets after 3 years?
For Mr. A his total assets are Rs29350.00 which implies an average
money-weighted return of -2.18% per annum.
For Mr. Bhis total assets are Rs844412.50 which implies an average
money-weighted return of 2.75% per annum.
Summary of
results
|
|
Scenario 1
|
Scenario 2
|
|
Time-Weighted Returns
|
2.81%
|
2.81%
|
|
Mr. A Money-Weighted Returns
|
8.35%
|
-2.18%
|
|
Mr. B Money-Weighted Returns
|
2.88%
|
2.75%
|
The reason for the big difference in money-weighted returns for
Mr. A is the fact that he had Rs0 in the first year and was therefore not
affected by the first years' results. When the negative return of -10% was
earned in the 1st year, he was not affected at all and only benefited from the
two positive years. However, when the negative year followed when his
accumulated assets was at its highest level i.e. in the last year, the effect
was devastating, bringing his total return into negative zone. This is because
now the return is not based on time, but on the amount of money it is applied
to. Hence the name "money-weighted"
returns.
As we can see, Mr.B was also affected but not as much as Mr. A.
The reason for this is that his assets in year 3 compared toher assets in year
1 was relatively similar which means that the effect of the returns was
similar, even though it was worseunder Scenario 2 when the negative return was
applied to a higher asset value.
Graphical
Representation of Calculation of TWRR and MWRR
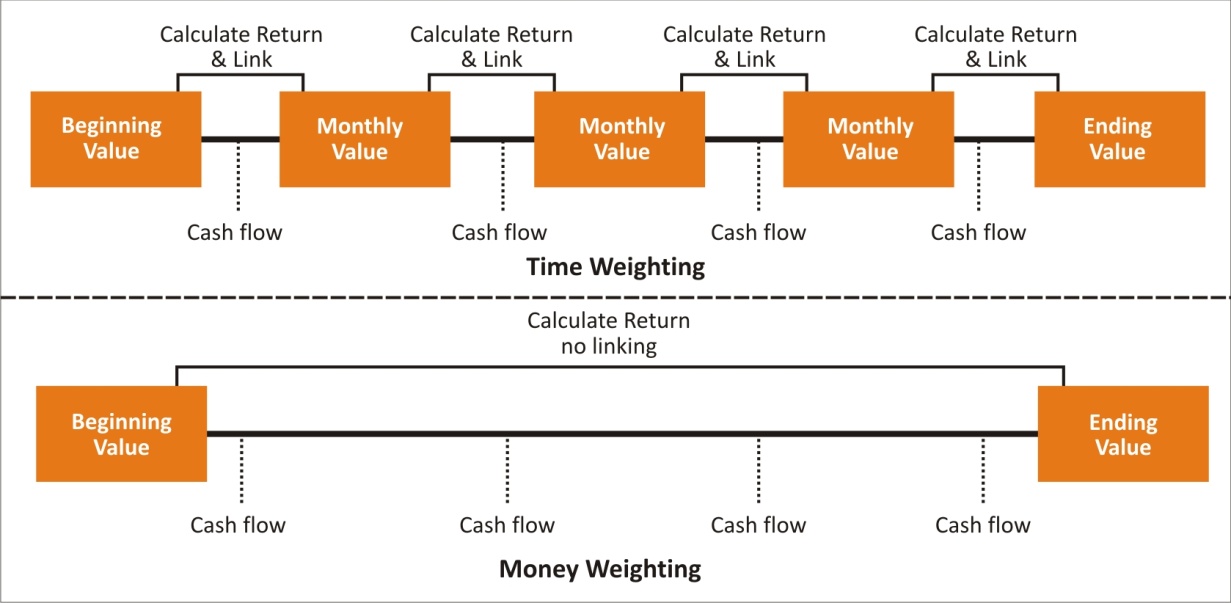
SNAPSHOT
|
Point of Distinction
|
TWR
|
IRR
|
|
Definition
|
Time Weighted Return measures the compound rate of
return over a given period for one unit of money.
|
A Money Weighted Return measures the compound growth rate
in the value of all funds invested in the account over the evaluation period.
|
|
Timing of Cash Flows
|
TWR is not affected by the timings of the external cash flows.
|
MWR is sensitive to the timing
of external cash flows
|
|
Usage
|
Time-weighted return is the superior measure for evaluating
public fund managers with no control over the
size or timing of cash
flows.
|
MWRR
is used for private fund managers because they typically exercise a degree of
control over the amount and timing of fund cash flows.
|
ADVANTAGES
AND DISADVANTAGES OF TIME AND MONEY WEIGHTED RETURNS
Advantages of using Money Weighted Rates of
Return:
Investors
can easily determine if they are making a consistent month on month return and
place an equivalent interest rate value on the return. If you are not
generating a consistent return, your internal rate of return will fall. There
can be no doubt about the importance of making a consistent return over time,
because as time goes by, the value of money depreciates due to the effects of
inflation.
Ideal for
comparing investment performance over time regardless of the size of the
investment or when you deposit or withdraw money; for example the Internal Rate of
Return is ideally suited to comparing the performance of stocks within a
portfolio, or comparing your portfolio with a given market index such as the
NIFTY or SENSEX.
Disadvantages of using Money
Weighted Rates of Return:
They are not suited to determining the change in the portfolio value
between two consecutive dates within a given date range.
Advantages of using Time Weighted
Rates of Return
It enables investors to determine rates of return independent of when
capital is added or withdrawn from the available investment fund. More commonly
this relates to fund managers and not private investors, as fund managers have
limited control over when they receive funds from investors, or when the
investor choose to withdraw their funds.
Ideally suited to environments where you have shared ownership, as they
enable ownership to be allocated based on the value of the assets and the
amount invested or withdrawn at any point in time.
Relatively simple to understand and calculate; for example when using the
Unit Valuation System the unit value is the sum of the assets divided by the
number of units in circulation. If you want to invest more money, you simply
buy more units at the current unit value. This is primarily used in all mutual
fund schemes.
Disadvantages of using Time
Weighted Rates of Return
They do not factor in how long money has been invested and therefore when
it was invested. As an investor, the Money Weighted Return measures, such as
the Internal Rate of Return enable you to track your performance over time. For
example the Unit Value might reflect that you have made a return of 100% but if
your unit value does not consistently increase, you can find yourself in a
position where your Internal Rate of Return is falling month after month, which
results in your investment capital devaluing with time.
Time Weighted metrics are not suited to comparing investment
performance for different investment portfolio.
....


